【摘要】求曲线上的动点到直线的距离的最值问题,这样的曲线常见的有圆,椭圆,双曲线,抛物线,以及函数图像。
Ⅰ:圆上的动点到直线的距离[点线距]的最值
如给定圆\(C:x^2+y^2=4\),和直线\(y=x+4\),求圆上任意一点到直线的距离[点线距]的最大值和最小值。
常用方法:
①几何方法,圆心到直线的距离为\(d\),则点线距的最大值为\(d+r\),最小值为\(d-r\);
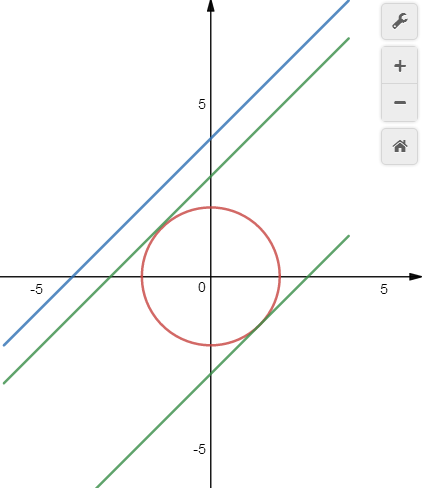
②平行线法,先设与已知直线平行且和圆相切的直线为\(y=x+m\),联立方程组,利用\(\Delta=0\)求得\(m\)的两个值,
则点线距的最小值为线线距中的最小值,其最大值为线线距中的最大值;
③参数方程法[或三角函数法],圆上任意一点坐标\((2cos\theta,2sin\theta)\),利用点到直线的距离公式转化为三角函数求最值;
其中以几何方法最为简单;
Ⅱ:椭圆上的动点到直线的距离[点线距]的最值
如给定椭圆\(C:\cfrac{x^2}{4}+\cfrac{y^2}{3}=1\),和直线\(y=x+4\),求椭圆上任意一点到直线的距离[点线距]的最大值和最小值。
常用方法:
①几何方法,失效;
②平行线法,先设与已知直线平行且和椭圆相切的直线为\(y=x+m\),联立方程组,利用\(\Delta=0\)求得\(m\)的两个值,则点线距的最小值为线线距中的最小值,其最大值为线线距中的最大值;
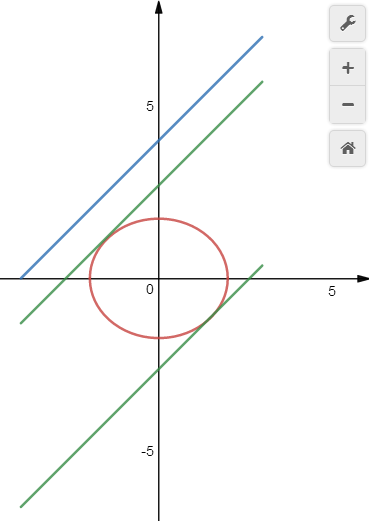
③参数方程法[或三角函数法],椭圆上任意一点坐标\((2cos\theta,\sqrt{3}sin\theta)\),利用点到直线的距离公式转化为三角函数求最值;
例02给定椭圆\(\cfrac{x^2}{3}+y^2=1\)和直线\(x+y-8=0\),已知点P是椭圆上的一个动点,求点P到直线的距离的最小值。
分析:首先易知椭圆和直线没有交点,即二者相离,从而可以考虑用椭圆的参数方程或平行线法求解。
法1、利用椭圆的参数方程,由椭圆方程\(\cfrac{x^2}{3}+y^2=1\)可知,
动点坐标\(P(\sqrt{3}cos\theta,sin\theta)\),
则点P到直线\(x+y-8=0\)的距离
\(d(\theta)=\cfrac{|\sqrt{3}cos\theta+sin\theta-8|}{\sqrt{2}}=\cfrac{|2sin(\theta+\cfrac{\pi}{3})-8|}{\sqrt{2}}\),
故当\(sin(\theta+\cfrac{\pi}{3})=1\)时,\(d_{min}=\cfrac{|2-8|}{\sqrt{2}}=3\sqrt{2}\);
\(sin(\theta+\cfrac{\pi}{3})=-1\)时,\(d_{max}=\cfrac{|-2-8|}{\sqrt{2}}=5\sqrt{2}\);
【问题】为什么不设点P的坐标为\((x,y)\)而采用参数坐标形式\((\sqrt{3}cos\theta,sin\theta)\)?
前者坐标形式是二元形式,后者是一元形式,故后者简单。
法2、平行线法,设和已知平行且和已知椭圆相切的直线\(x+y+m=0\),
则由\(x+y+m=0\)和\(\cfrac{x^2}{3}+y^2=1\),消去\(y\)可得\(4x^2+6mx+3m^2-3=0\),
由二者相切可知,\(\Delta=36m^2-4\times4(3m^2-3)=0\),解得\(m=\pm 2\),
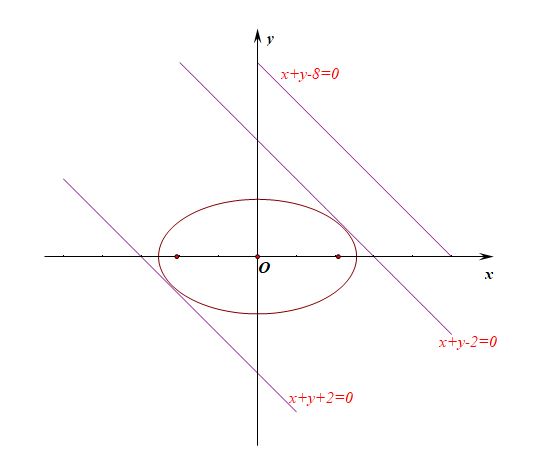
即和椭圆相切的直线有\(x+y-2=0\)和\(x+y+2=0\),故切点到直线\(x+y-8=0\)的距离就可以用两条平行线间的距离来刻画,
则\(d_{max}=\cfrac{|2-(-8)|}{\sqrt{2}}=5\sqrt{2}\),\(d_{min}=\cfrac{|-2-(-8)|}{\sqrt{2}}=3\sqrt{2}\)。
Ⅲ:抛物线上的动点到直线的距离[点线距]的最值
如给定抛物线\(C:y^2=4x\),和直线\(y=x+4\),求抛物线上任意一点到直线的距离[点线距]的最大值和最小值。
常用方法:
①几何方法,失效;
②平行线法,先设与已知直线平行且和抛物线相切的直线为\(y=x+m\),联立方程组,利用\(\Delta=0\)求得\(m\)的一个值,
则线线距即为所求的点线距的最小值;
③参数方程法[或二次函数法],由抛物线的参数方程,比如其上任意一点坐标\((2s^2,2\sqrt{2}s)\),利用点到直线的距离公式转化为二次函数求最值;
例03在平面直角坐标系\(xoy\)中,已知直线\(l\)的参数方程是\(\begin{cases}x=-8+t\\y=\cfrac{t}{2}\end{cases}(t为参数)\),
曲线\(C\)的参数方程是\(\begin{cases}x=2s^2\\y=2\sqrt{2}s\end{cases}(s为参数)\),设\(P\)为曲线\(C\)上的动点,求点\(P\)到直线\(l\)的距离的最小值。
分析:直线\(l\)的直角坐标方程是\(x-2y+8=0\),曲线\(C\)上的动点\(P\)的坐标\((2s^2,2\sqrt{2}s)\),
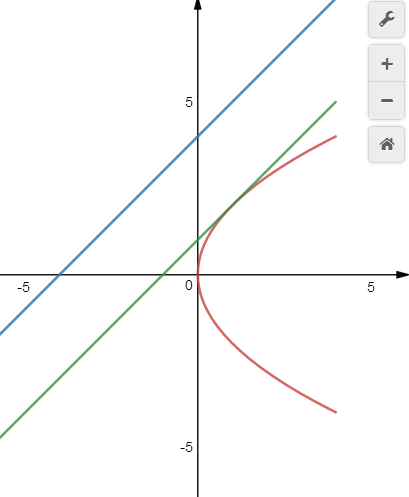
则由点到直线的距离公式可得,
\(d=d(s)=\cfrac{|2s^2-4\sqrt{2}s+8|}{\sqrt{1^2+(-2)^2}}\)
\(=\cfrac{|2(s-\sqrt{2})^2+4|}{\sqrt{5}}\)
当\(s=\sqrt{2}\)时,\(d_{min}=\cfrac{4\sqrt{5}}{5}\)。
Ⅳ:函数图像上的动点到直线的距离[点线距]的最值
常用方法:
①几何方法,失效;
②平行线法[切线法],先设与已知直线平行且和抛物线相切的直线为\(y=x+m\),此时不能利用\(\Delta=0\)求解,
只能用切线法,则线线距即为所求的点线距的最小值;
③参数方程法,失效;
例04
直线\(y=x\)上的动点为\(P\),函数\(y=lnx\)上的动点是\(Q\),求\(|PQ|\)的最小值。【等价题目】直线\(y=x\)上的点为\(P(x,y)\),函数\(y=lnx\)上的点是\(Q(m,n)\),求\(\sqrt{(x-m)^2+(y-n)^2}\)的最小值。
思路:平行线法,设和直线\(y=x\)平行且和函数\(y=lnx\)相切的直线为\(y=x+m\),
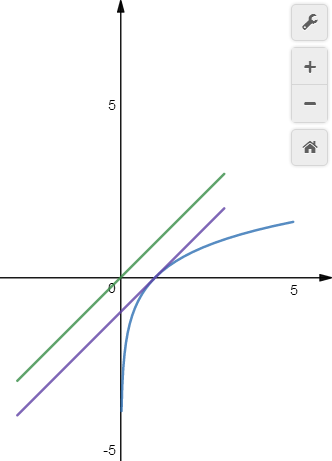
切点为\(P_0(x_0,y_0)\),则有
\(\begin{cases} y_0=x_{0}+ m \\ y_0=lnx_0 \\ f'(x_0)=\cfrac{1}{x_0}=1\end{cases}\);
从而解得\(x_0=1,y_0=0,m=-1\)
所以所求的点点距的最小值,就转化为切点\(P_0(1,0)\)到直线\(x-y=0\)的点线距,
\(d=\cfrac{|1-0|}{\sqrt{1^2+1^2}}=\cfrac{\sqrt{2}}{2}\)。
或者两条直线\(y=x,y=x-1\)的线线距\(d=\cfrac{|1-0|}{\sqrt{1^2+1^2}}=\cfrac{\sqrt{2}}{2}\)。
对应练习
练1已知点\(M\)在圆\(C:x^2+y^2-4y+3=0\)上,点\(N\)在曲线\(y=1+lnx\)上,则线段\(MN\)的长度的最小值为\(\sqrt{2}-1\)。
练1